本文摘要:我們介紹選擇權希臘字母Delta。為什麼要有懂Delta?Delta的意義是什麼?我們並討論如何快速預估Delta?不需透過複雜的公式計算,你也可以掌握Delta變化,有效控制風險!
為什麼要討論Delta?
許多剛接觸選擇權的朋友,最熟悉的應該是買買權(Buy CALL, Long CALL)。買買權代表看漲。大盤漲了,買買權就可能會賺錢。但大家有沒有想過:"買買權看漲" 是一個很粗糙的講法。因為看大盤會漲,所以買進買權。假設大盤真的漲了,漲了100點,買權也會跟著漲100點嗎?
有做過選擇權交易的玩家應該都很清楚,事情不是那麼簡單。
選擇權屬於衍生性金融商品,指數選擇權的標的物(Underlying)就是大盤加權指數。大盤漲跌可能會與買權漲跌同步,但卻不是1:1的比例同步漲跌。
我們說的更精確點:假設大盤漲x點, CALL會跟著漲 y點;或著,大盤跌x點,CALL會跟著跌y點。 只是,x與y之間的關係,我們怎麼去描述?
聰明的數學家於是導出了x與y之間的關係:Delta,這個希臘字母代表著x與y之間的比例,也就是 Delta = y/x。
簡單的說,Delta這個參數,代表著大盤每漲1點,選擇權權利金點數的變化量。
圖一為2013年8月7日選擇權盤中價位表。中間是履約價,左邊是買權(CALL),右邊是賣權(PUT)。
我們可發現7900CALL的Delta為0.889,這代表著如果我今天買一口7900CALL@61點,花了3050元的權利金,當大盤漲10點,則CALL也會跟著漲10×0.8896點,粗略的估計為8點或9點,則7900CALL的權利金將會來到69或70點(61+8 or 61+9)。
 |
| 圖一:2013年08月07日選擇權盤中價位 (資料來源:永豐 e-Leader) |
螞蟻的角度看世界:談Delta的精確度
圖二為某檔買權價格(C)與大盤指數(S)的關係圖,紅色曲線為買權的價格曲線,橫軸為加權指數S,縱軸為買權價格C。若當時大盤價位在8000點,我們在8000點劃一條切線(橘色三角形斜邊),則通過8000點(藍色圓點)的切線斜率即為當時的 Delta值。
由圖二可知,8000點的切線斜率為0.74,讀者可以詮釋成大盤指數波動100點 (公平起見左右各50點),則買權價格會相對應波動74點。然而,是不是真的大盤漲了100點,買權價格就會漲74點,不見得!
看Delta=0.74這件事,我們必須從螞蟻的角度看世界。在螞蟻的世界裡,再彎的曲線都像是直線。所以嚴謹的說,Delta=0.74代表著大盤漲跌1點,買權價格約漲跌0.74點。
由圖二可知,8000點的切線斜率為0.74,讀者可以詮釋成大盤指數波動100點 (公平起見左右各50點),則買權價格會相對應波動74點。然而,是不是真的大盤漲了100點,買權價格就會漲74點,不見得!
看Delta=0.74這件事,我們必須從螞蟻的角度看世界。在螞蟻的世界裡,再彎的曲線都像是直線。所以嚴謹的說,Delta=0.74代表著大盤漲跌1點,買權價格約漲跌0.74點。
 |
| 圖二:買權價格曲線 (大盤價位8000點) |
如果下一個時刻大盤跌了50點,來到7950點的價位,買權價格曲線在7950點的切線斜率變為0.44,此時意味著大盤毎波動1點,買權價格會波動0.44點。(如圖三所示)
注意到,這些敘述都是在描速買權價格在 "這個時刻"、"這個價位" 相對應大盤的波動。一旦大盤真的上漲或下跌,不同履約價買權的價格曲線受到波動度的影響,也可能跟著改變。
這也是牧清華所說,看選擇權的價格變動,或是Delta所代表的切線斜率,要從螞蟻的角度看世界,越小隻的螞蟻,視野中看到的越局部,彷彿時間靜止、眼前的價格變動不再是曲線,而是直線 (7950點的切線)。
注意到,這些敘述都是在描速買權價格在 "這個時刻"、"這個價位" 相對應大盤的波動。一旦大盤真的上漲或下跌,不同履約價買權的價格曲線受到波動度的影響,也可能跟著改變。
這也是牧清華所說,看選擇權的價格變動,或是Delta所代表的切線斜率,要從螞蟻的角度看世界,越小隻的螞蟻,視野中看到的越局部,彷彿時間靜止、眼前的價格變動不再是曲線,而是直線 (7950點的切線)。
 |
| 圖三:買權價格曲線 (大盤價位7950點) |
如何預估Delta?(割線逼近切線)
瞭解Delta的概念後,我們當然想知道Delta是如何計算出來?當然,理論上是經由選擇權評價公式推導而來(買權價格對大盤指數的一階微分),然而公式複雜不容易計算,若您想要馬上就看出某檔履約價買權的Delta值,是否有快速計算的方法?以上的問題,我們可由割線逼近切線的方式去預估切線斜率。如圖四所示,若大盤價位在8000點,下一刻來到了8050點,由圖可知買權價格為112點 (根據當時的買權價格曲線)。
同樣的,如果大盤下一刻來到7950點,買權價格為40點。將這兩點的價位(紅圈黃底)連接起來的割線(圖四藍色虛線),是不是其傾斜的程度與過8000點個切線(三角型斜邊)幾乎一樣?
 |
| 圖四:買權價格曲線 (用割線逼近切線預估 Delta) |
快速計算Delta值
可惜的是,當大盤在8000點價位時,我們並不知道大盤瞬間漲到8050點或是7950點時的買權價位。這裡,牧清華提供一個估計大盤來到8050點與7950點時,買權價位的方法。
我們拿2013年08月08日當例子,如圖五所示,大盤當時價位7910點,8000CALL價位20點,我們想要估計8000CALL的Delta值。
根據圖四概念,大盤價位若是漲50點來到7960點,則8000CALL應該要漲到35點。理由是大盤漲50點後,8000CALL的新價位應近似於過去7950CALL的價位(35點)。
同理,另一方面,大盤價位若是跌50點來到7860點,則8000CALL應該要跌到10點,即為原本8050CALL的價位。
我們拿2013年08月08日當例子,如圖五所示,大盤當時價位7910點,8000CALL價位20點,我們想要估計8000CALL的Delta值。
根據圖四概念,大盤價位若是漲50點來到7960點,則8000CALL應該要漲到35點。理由是大盤漲50點後,8000CALL的新價位應近似於過去7950CALL的價位(35點)。
同理,另一方面,大盤價位若是跌50點來到7860點,則8000CALL應該要跌到10點,即為原本8050CALL的價位。
所以預估8000CALL的Delta值為 (35-10) /100 = 0.25,事實上跟理論推估出來的Delta 0.32 (如圖五所示)有些出入,但天知道實際上到底是理論估計值準還是牧清華提供的方法準?
注意唷~ 用這個方法,推估7900CALL的 Delta為 (86-35)/100 = 0.51,與理論估計值0.5092幾乎一樣!神奇吧?以上只是很快速計算Delta的方法,誤差難免有。那有沒有又快速又精確的方法?牧清華:【有的,未來有機會介紹!】
注意唷~ 用這個方法,推估7900CALL的 Delta為 (86-35)/100 = 0.51,與理論估計值0.5092幾乎一樣!神奇吧?以上只是很快速計算Delta的方法,誤差難免有。那有沒有又快速又精確的方法?牧清華:【有的,未來有機會介紹!】
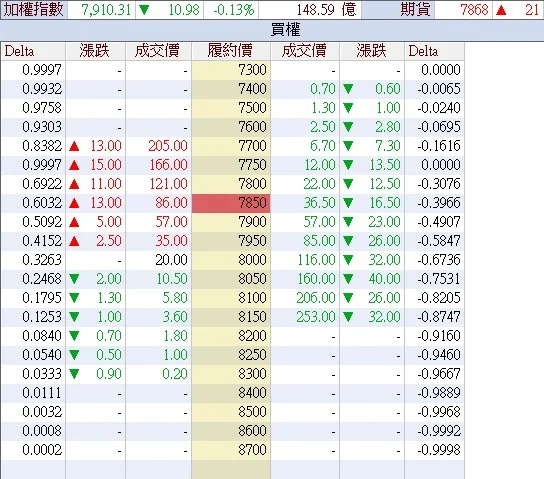 |
| 圖五:選擇權價位與Delta值 (資料來源:永豐 e-Leader) |
別太相信定價理論,有時真實數據從市場上反映出來的訊息更為重要。
喔~ 不,不是更為重要?!在金融交易市場上,真實絕對比理論重要!
